| Study | Effect expected | N | Trials | M | SD | Hits (%) | t | p | ES | Var | BF | Direction | Year | Lab/Online |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
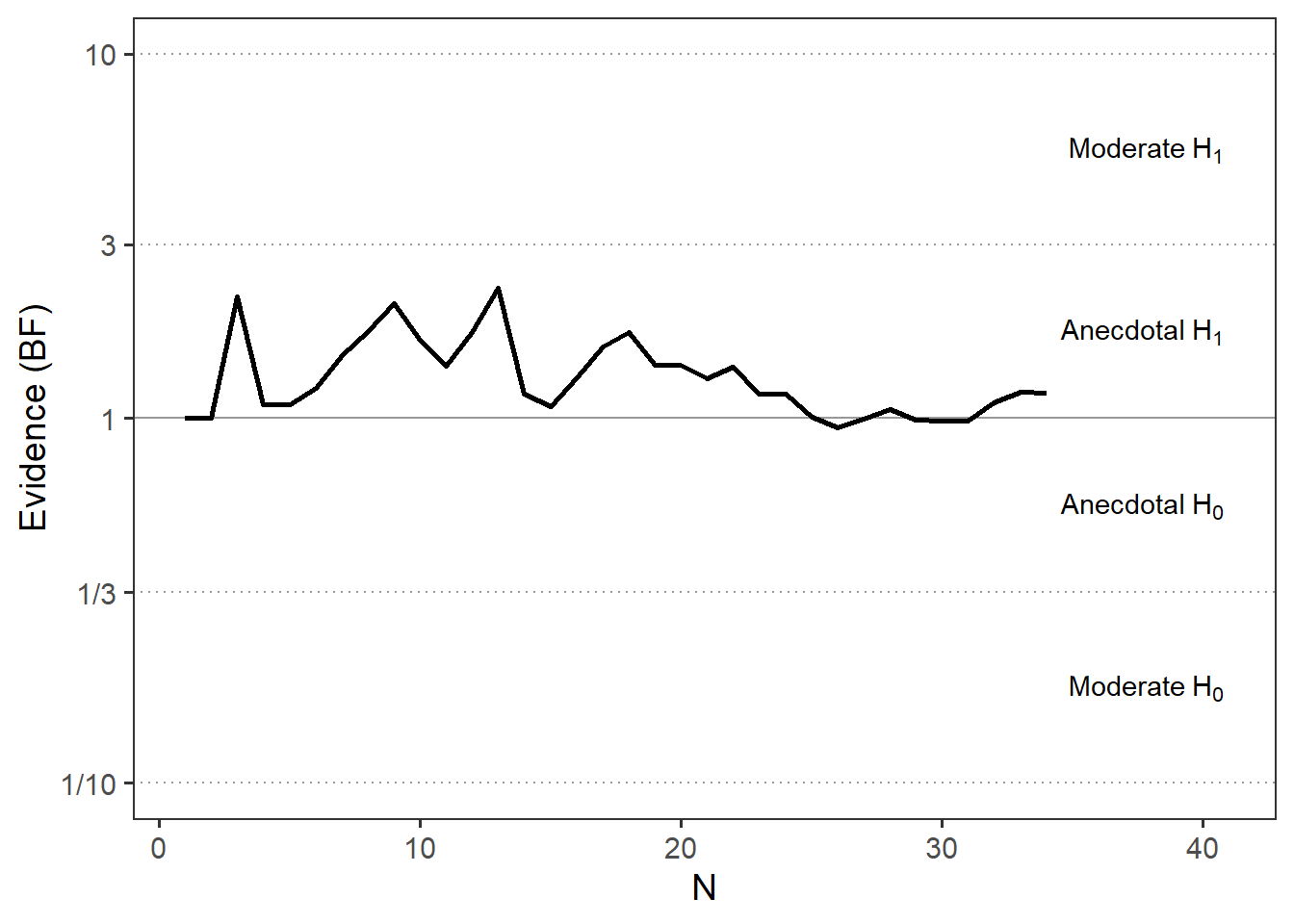
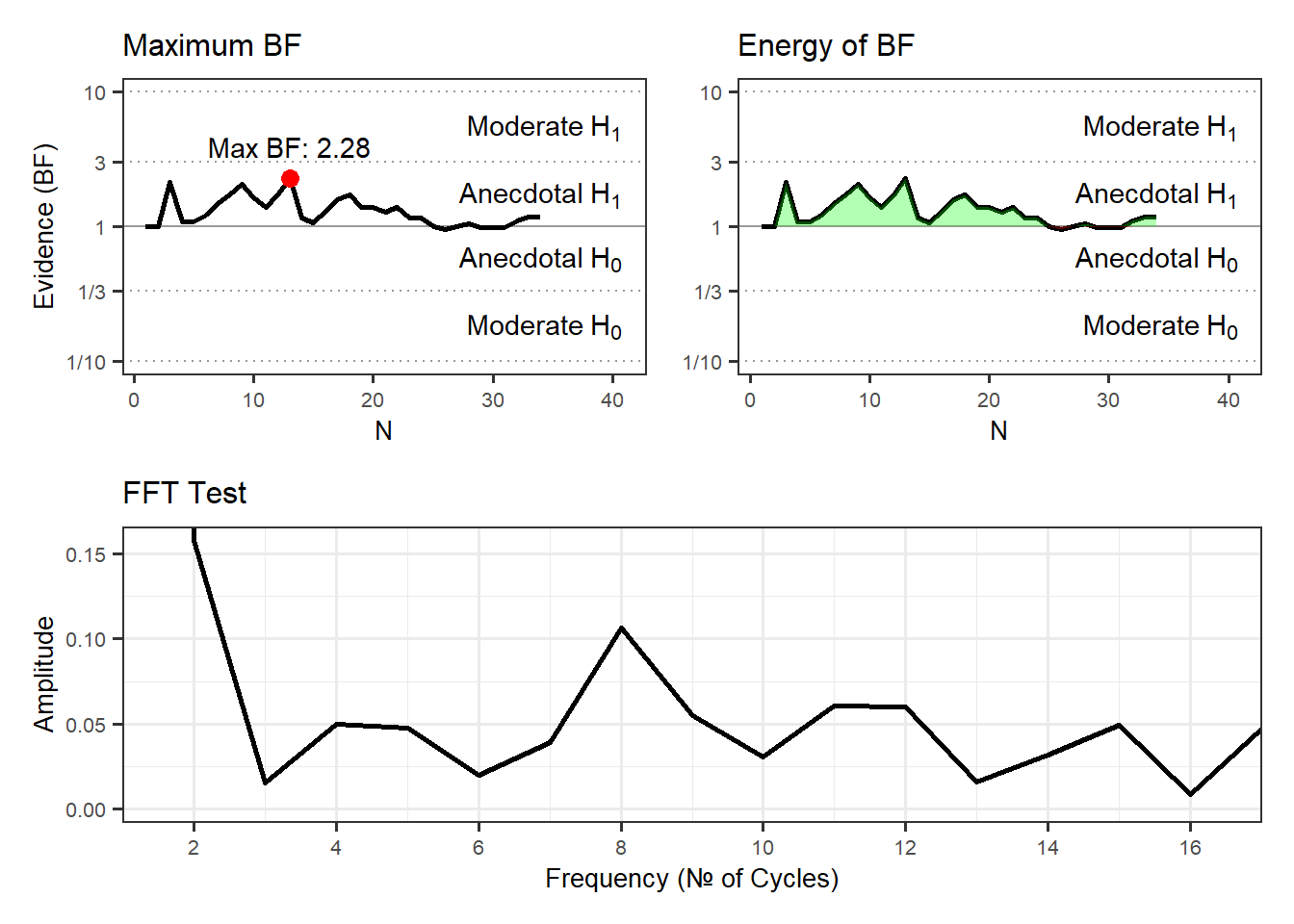
| Robots | ✔ | 34 | 10 | 5.29 | 1.66 | 52.94 | 1.03 | 0.15 | 0.18 | 0.03 | 1.18 | greater | 2023 | 🌍 |
Robots
Hypothesis
In this experiment, we investigated whether it is possible to reduce the typically large sample sizes required in micro-psychokinesis (micro-PK) research by extending the classical system of one person interacting with one quantum random number generator (qRNG) to a system in which one person is linked to multiple qRNGs.
Our central hypothesis was that participants could influence the outcome of qRNGs more effectively when their mind was meaningfully connected to multiple qRNGs, as opposed to just one. To test this, we designed a roulette game in which participants were assigned to either an experimental or a control group. In both groups, the participants placed bets on red or black. However, only in the experimental group did the outcomes from an additional 99 qRNGs (representing robot clones of the player) contribute to the total winnings shown to the participant. In the control group, these extra qRNGs were also run but their outcomes were hidden and irrelevant to the player’s reward. If a meaning-based connection as proposed by the unus mundus theory holds, only the qRNGs that were meaningful to the participant—that is, those in the experimental group—should be susceptible to induced correlations.
We hypothesized (H1) that both groups might show positive deviations from chance due to mind-matter interactions, but the experimental group would show a faster and stronger effect. Furthermore (H2), we expected that the experimental group would outperform the control group in total effect strength. Exploratorily, we also examined whether factors such as roulette experience, age, gender, and motivation to win would modulate the strength or presence of the effect.
Participants
| Characteristic | Count/Statistic |
|---|---|
| N | 34 |
| Female | 67.65% |
| Male | 26.47% |
| Mean Age | 27.26 years |
| SD Age | 12.65 years |
Materials and Procedure
Participants accessed the online experiment via a link shared through social networks. Upon opening the link, they first saw an instruction page tailored to their group (experimental or control), followed by a visual example of how the game worked. After confirming their understanding and accepting the privacy policy, they proceeded to the experiment.
Each participant played ten rounds of a roulette game, where they were asked: “Which color would you like to bet on?” and chose between red or black. The outcome of each round was determined by a qRNG, and the result was immediately shown on-screen. Participants were also shown their updated total winnings and whether their choice matched the randomly selected color. If correct, they gained money; otherwise, they did not. Losses were set to zero, so participants could only win or break even.
The crucial difference between the two groups was the visibility and relevance of the additional qRNGs:
In the experimental group, the results from 99 additional roulette tables (each controlled by its own qRNG) were shown and counted toward the participant’s total winnings. These additional outcomes were tied to the participant’s chosen color and presented as if generated by “robot clones.”
In the control group, these extra qRNGs were also run, but their outcomes were not shown and had no bearing on the participant’s winnings.
After the roulette game, participants filled out a brief questionnaire including their age, gender, familiarity with roulette, and how important winning was to them (on a 1–7 scale). Finally, they saw a closing screen with instructions on how to claim any winnings.
Sample Size and Data Analysis
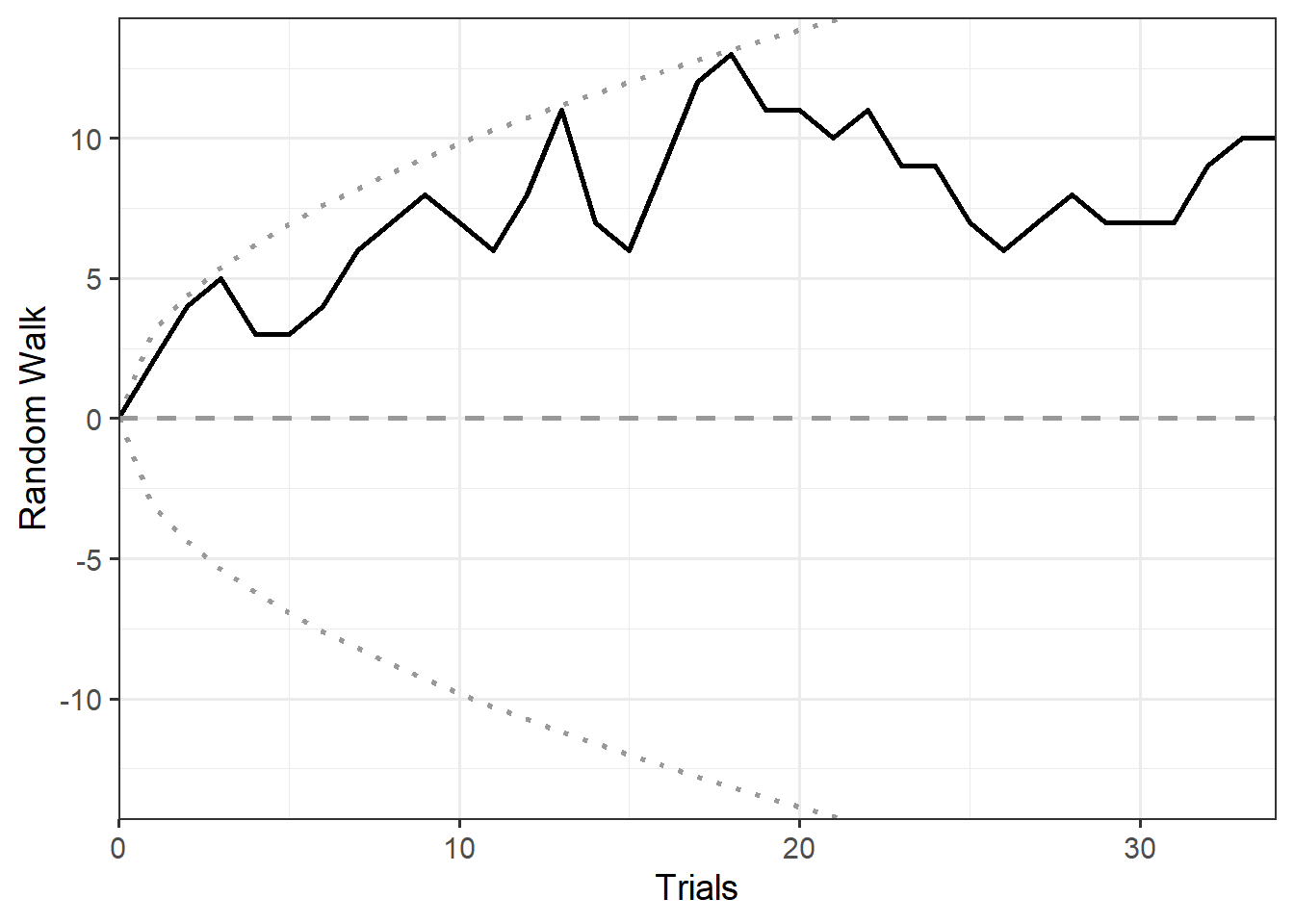
The primary goal was to explore whether the proposed design—linking one person to multiple qRNGs—could yield detectable effects even with a small number of participants. Therefore, no power analysis or fixed endpoint was set. Instead, we employed Bayesian sequential analysis, which allows data collection to continue until sufficient evidence is reached for or against a hypothesis, based on the accumulation of data.
To calculate Bayes Factors, we used a Cauchy distribution centered around zero with a scale parameter r = 0.1, reflecting a small expected effect size (Cohen’s d ≈ 0.1). This prior distribution is consistent with earlier micro-PK research by the same working group.
We used RStudio and JASP for all analyses, including data preparation, descriptive statistics, group comparisons, and t-tests. In addition to the main hypothesis tests, we conducted exploratory subgroup analyses (e.g., by age, gender, and importance of winning) and linear regressions to examine possible trends over time or by participant order.
Lab Report Data
For this lab report only the human subjects’ scores of both conditions are considered.
Results of Universal Micro-PK Hypothesis