| Study | Effect expected | N | Trials | M | SD | Hits (%) | t | p | ES | Var | BF | Direction | Year | Lab/Online |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baseline 2 | ✔ | 2094 | 20 | 12.02 | 2.19 | 49.93 | 0.37 | 0.64 | 0.01 | 0 | 0.13 | less | 2024 | 🌍 |
Baseline 2
Hypothesis
This preregistered replication study focused exclusively on testing the micro-PK effect found in the “lucky” condition of the Baseline 1 study. We hypothesized that participants in this micro-PK study would demonstrate fewer hits in a coin toss game than expected by chance when the probability of winning is pre-set at 60%. Specifically, we predicted that the average number of hits in a series of 20 coin tosses would be lower than 12, which is the expected number of hits given the 60% pre-set winning probability.
Our theoretical justification remained consistent with the previous study: we reasoned that participants’ implicit beliefs and expectations about coin tosses being fair (expecting a 50% hit rate) would bias the quantum random number generator outcomes during their observations. If participants’ fairness expectations actively influence reality construction through micro-PK abilities, we should observe a substantial deviation from the 60% baseline toward their expected 50% probability. This study aimed to provide insights into whether participants’ micro-PK abilities are influenced by their fairness expectations and whether these expectations lead to measurable effects on quantum randomness.
Participants
| Characteristic | Count/Statistic |
|---|---|
| N | 2094 |
| Female | 58.55% |
| Male | 40.31% |
| Mean Age | 32.27 years |
| SD Age | 45.59 years |
Materials and Procedure
The procedure was identical to the lucky subsample of the previous study with the following key specifications: We used the same 20-round coin toss game where participants guessed the outcome of each flip, with outcomes determined by a quantum random number generator (qRNG) that generated numbers between 0 and 99 for each trial. A hit occurred when the generated number was below 60, ensuring a 60% hit probability that remained hidden from participants, who believed they were playing a fair coin toss game.
However, this replication study streamlined the measurement approach. We measured potential predictors and covariates including beliefs about chance, experience with probability, and both explicit and implicit knowledge of probability (assessed through a sequence production task). Nonetheless, the focus remained primarily on the main behavioral outcome.
Sample Size and Data Analysis
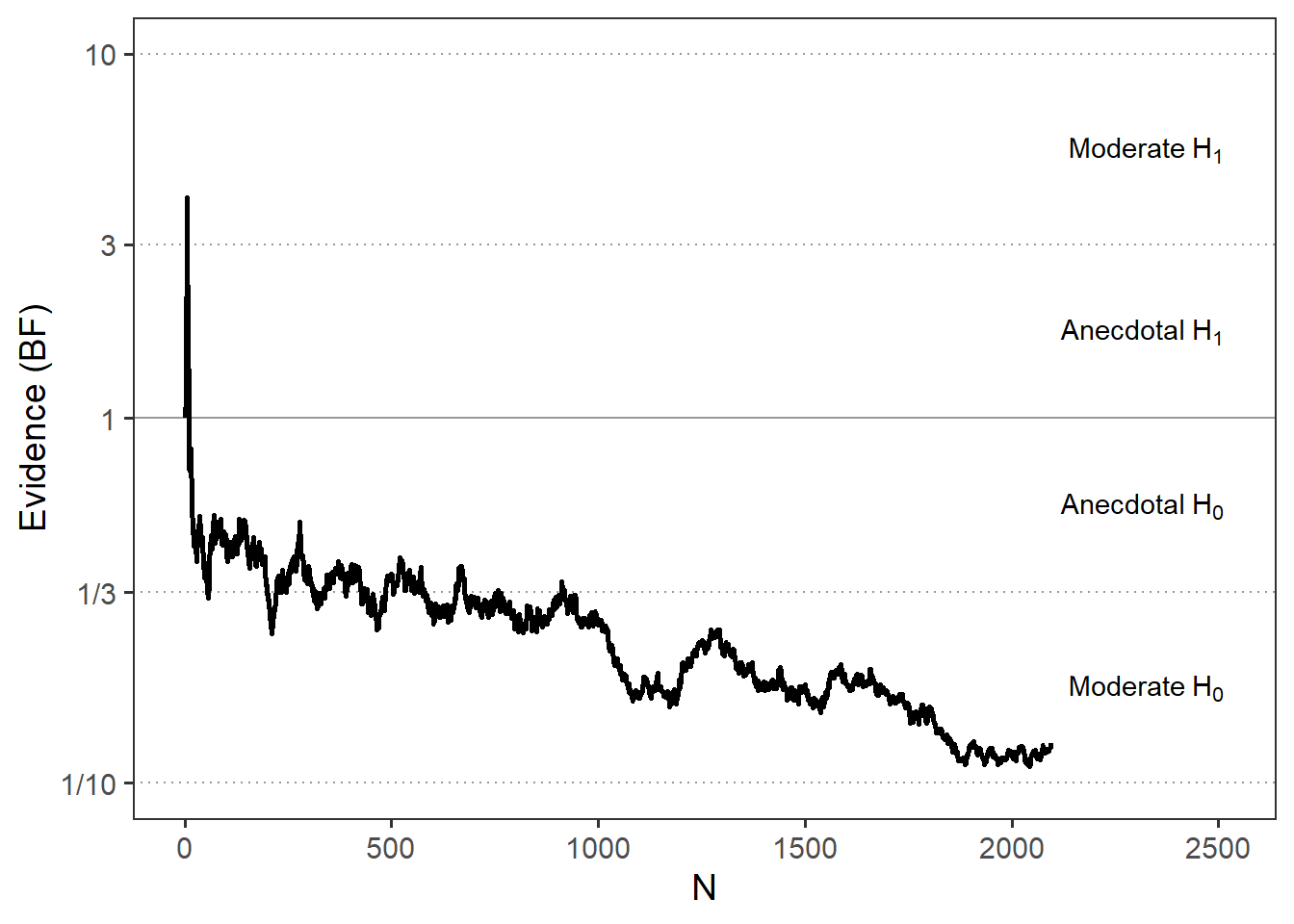
We employed a Sequential Bayesian design with a maximum sample size of 2,000 participants (based on a Bayes Factor Design Analysis).
Our statistical analysis used a Bayesian one-sample t-test with a Cauchy(0, 0.1) prior distribution, testing the directional hypothesis that participants would achieve fewer than 12 hits out of 20 coin tosses. We set our stopping criteria at a Bayes Factor of 10 or greater for strong evidence in favor of either the alternative hypothesis (H1) or null hypothesis (H0). We did not reach that point but stopped data collection after accumulating a little over our specified maximum N.
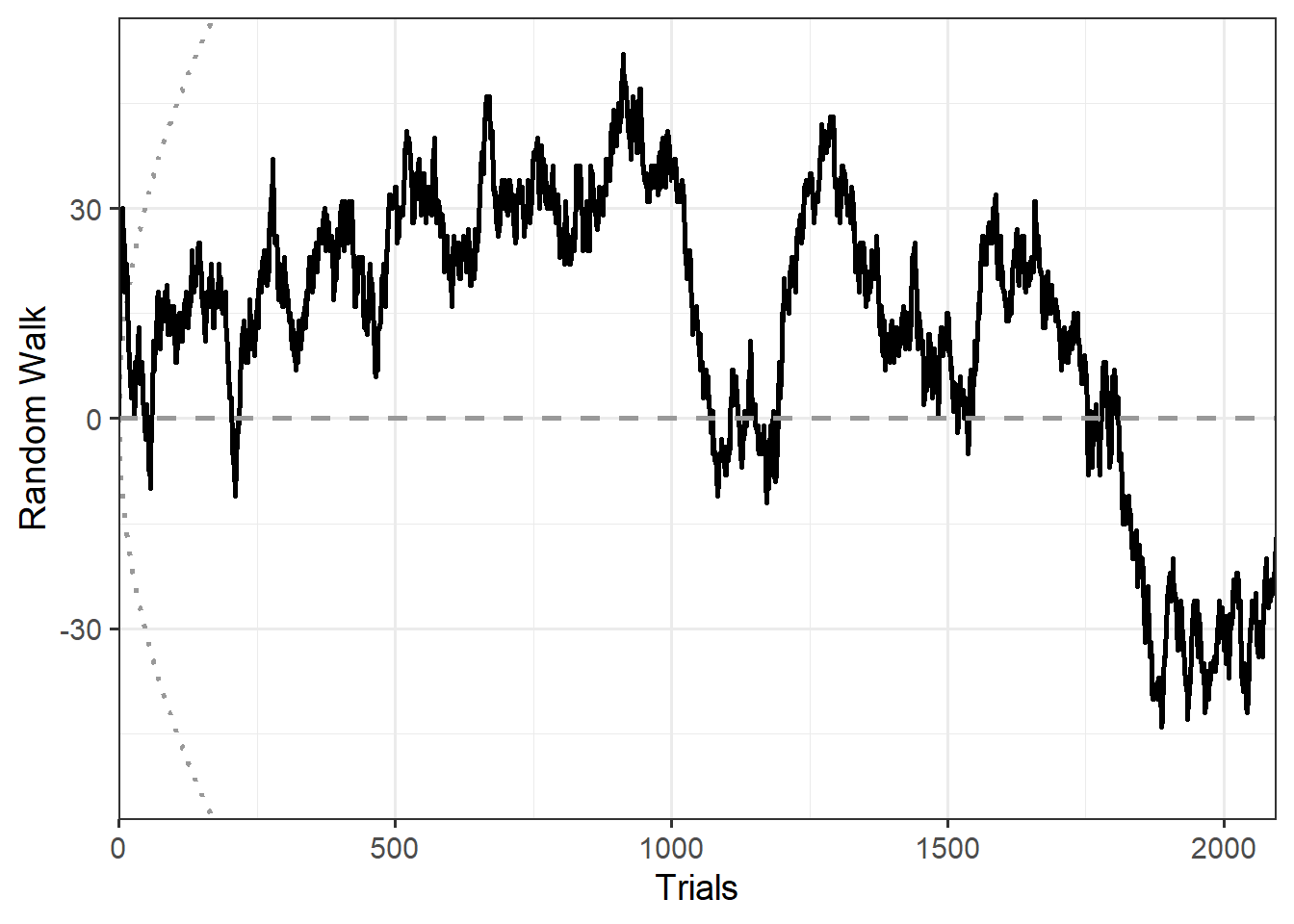
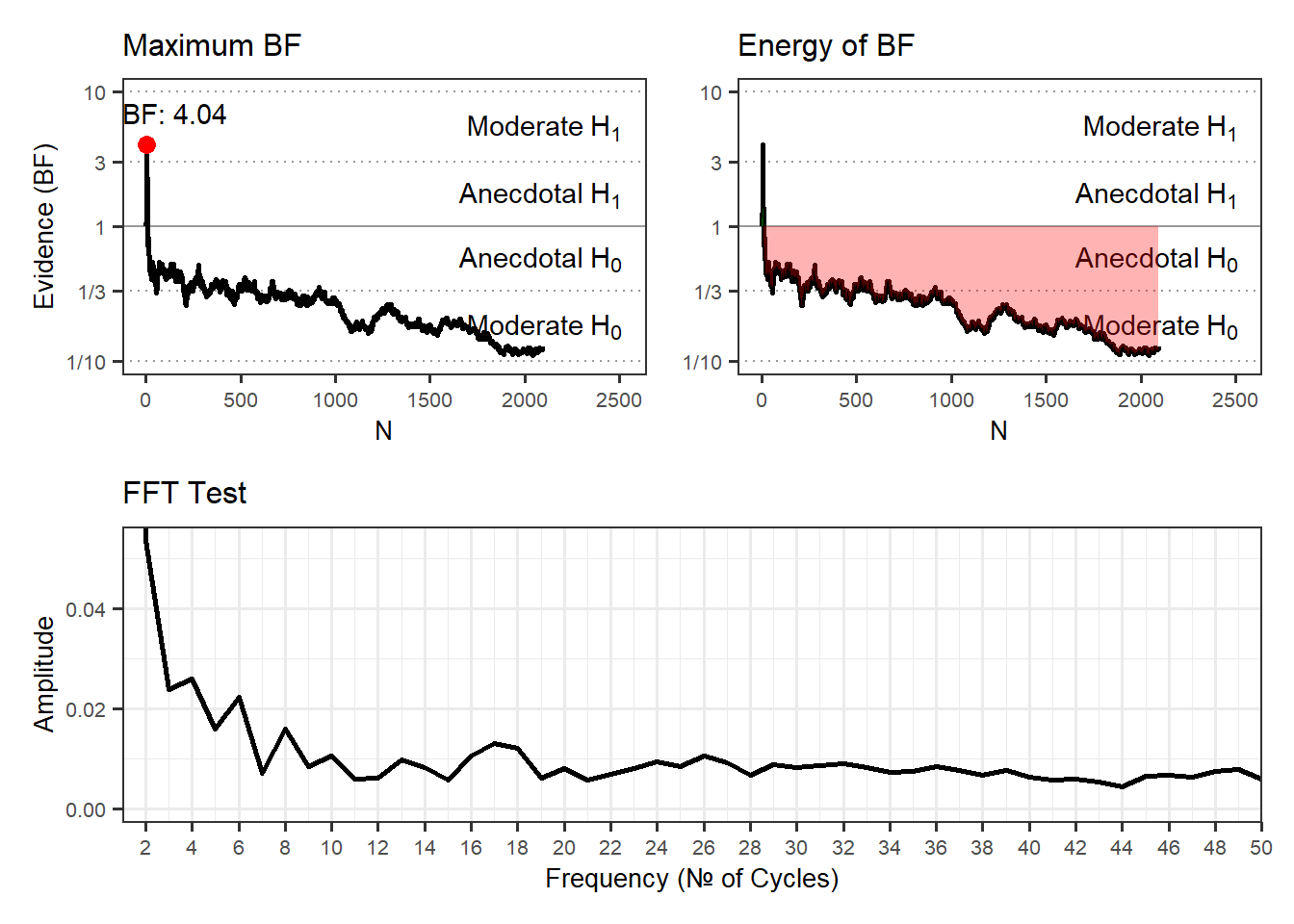
Results of Universal Micro-PK Hypothesis
- Publication (in preparation)
- OSF Project
- Experimental Program
- Coin Stimuli