CoE Meta-Analysis

Last update: 14 July 2025

Meta-Analysis of Change of Evidence Measures

In these meta-analyses, we will analyze the overall significance of the change of evidence-measures in all experimental and control studies. Since we don’t have effect sizes for these measures, we will combine the empirical p-values of the studies, this means, we will analyze the amount of simulations that show an equal or higher value in the maxbf, energybf, and frequency tests than the empirical BF.

The resulting p-values will be analyzed using the inverse chi-square method, which converts each p-value into a chi-square statistic and then sums them up. The method allows for the incorporation of different degrees of freedom, making it particularly useful when the p-values come from tests with varying sample sizes.

In this analysis all Micro-Pk studies of the LMU Micro-Pk Lab are included that hypothesize the presence of an effect. In studies comparing experimental to control conditions, only the experimental conditions are included.

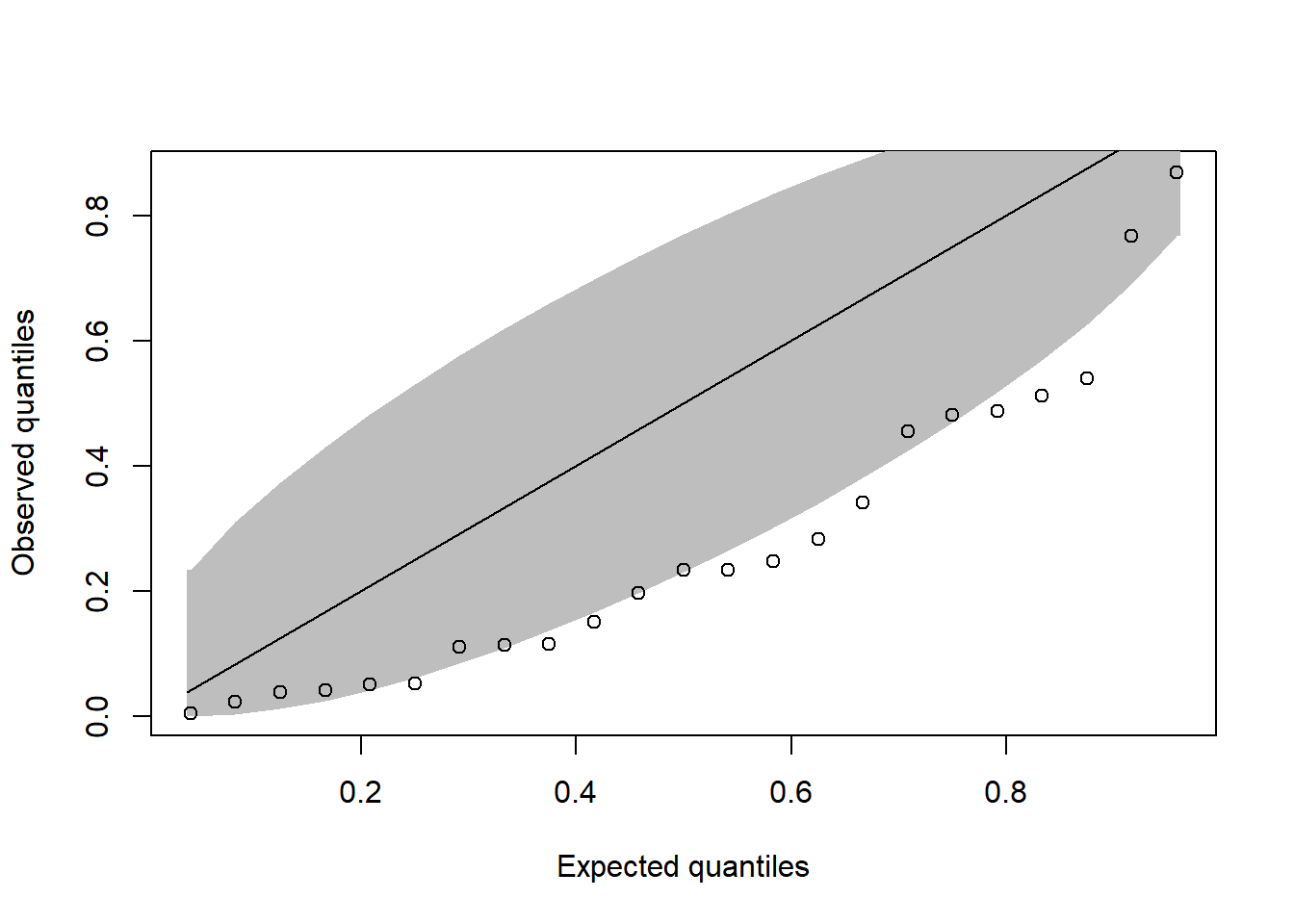
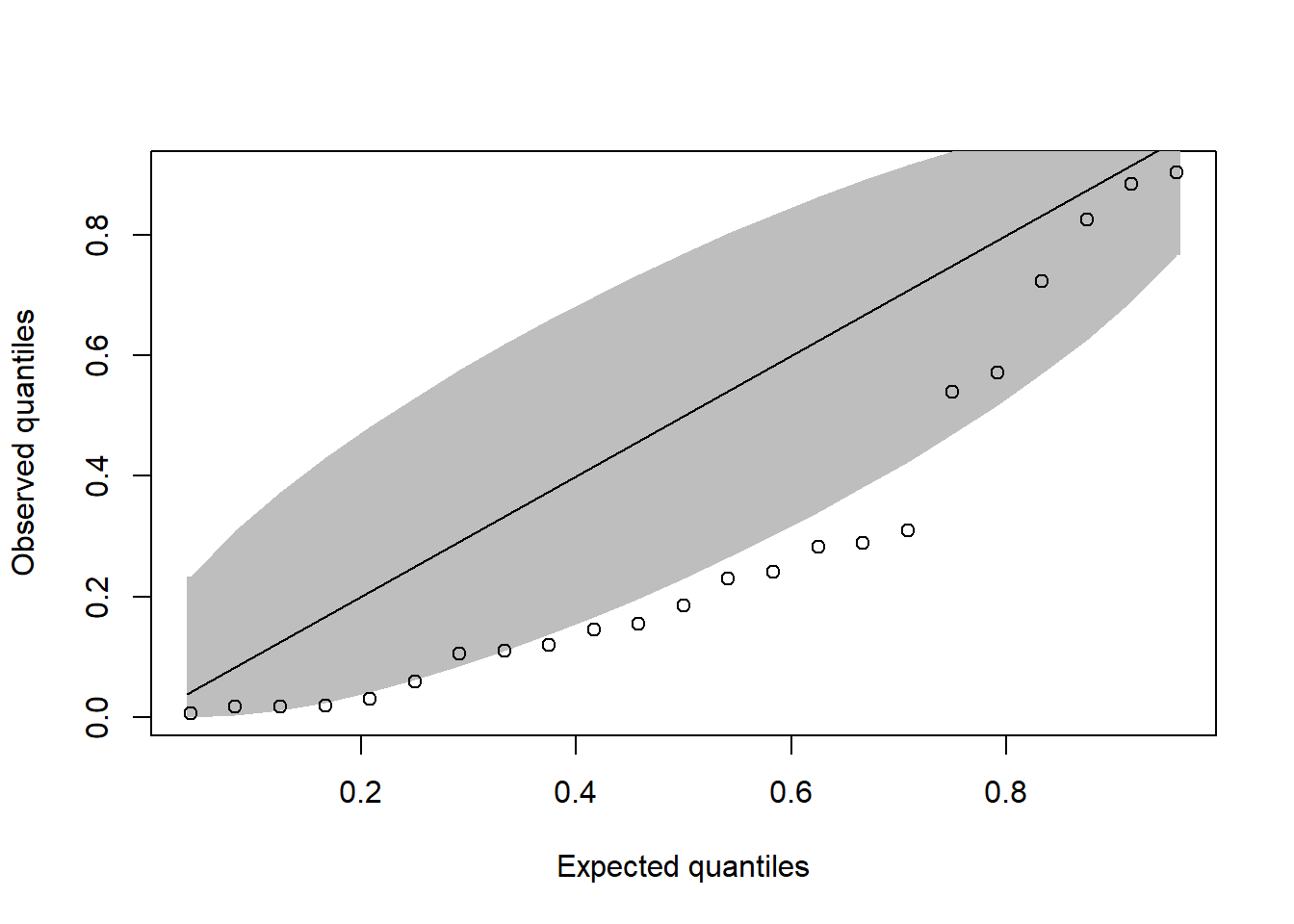
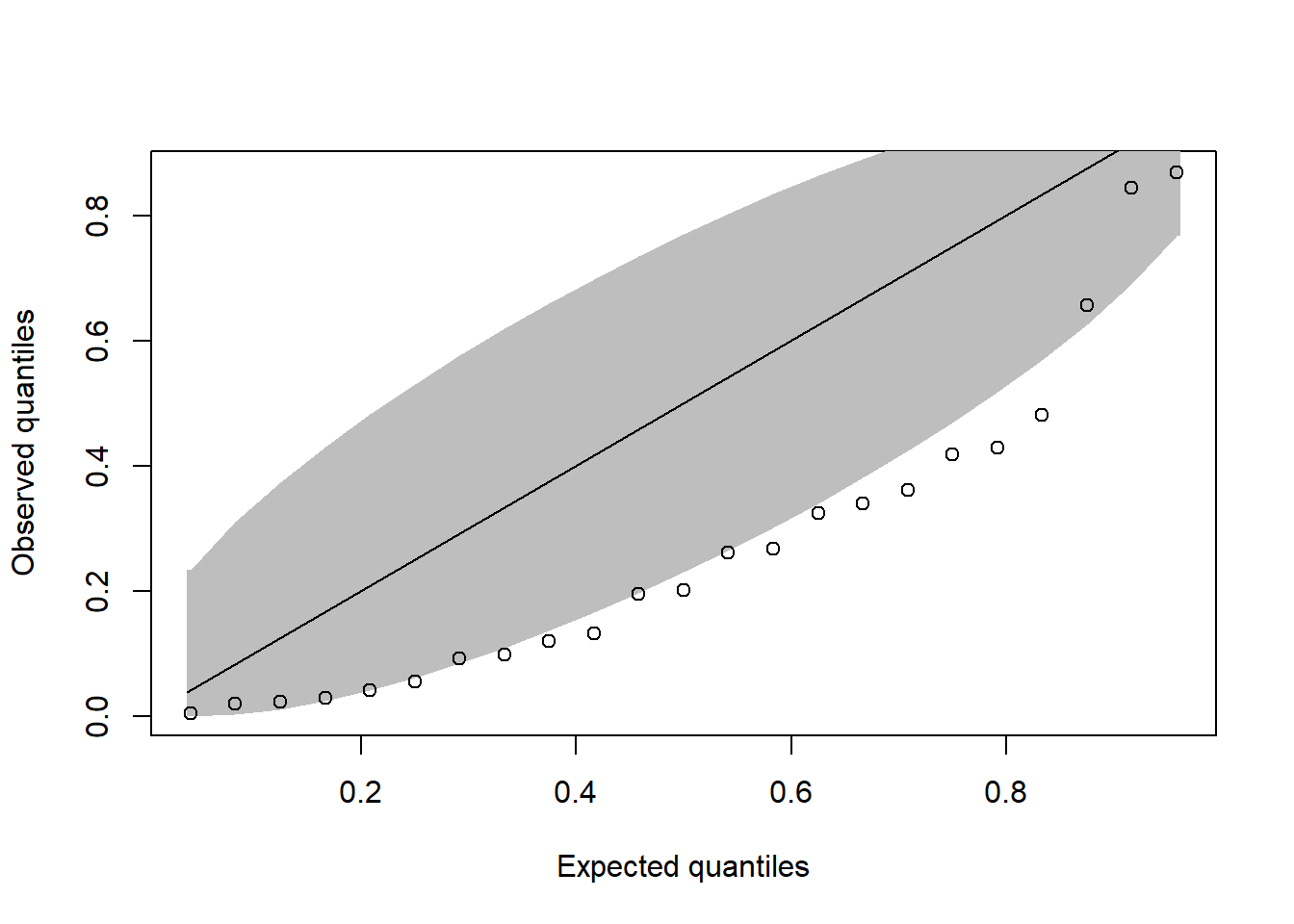
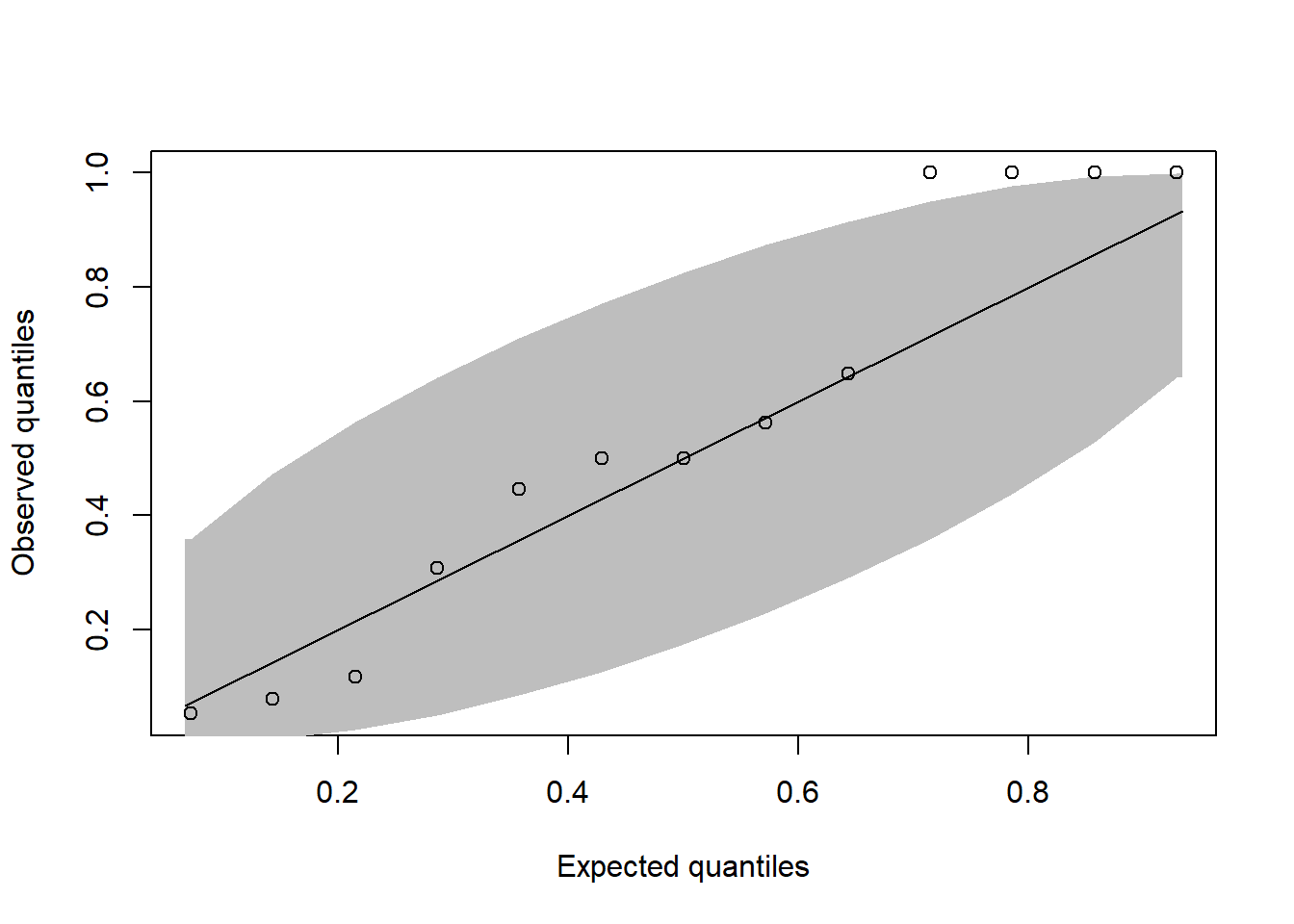
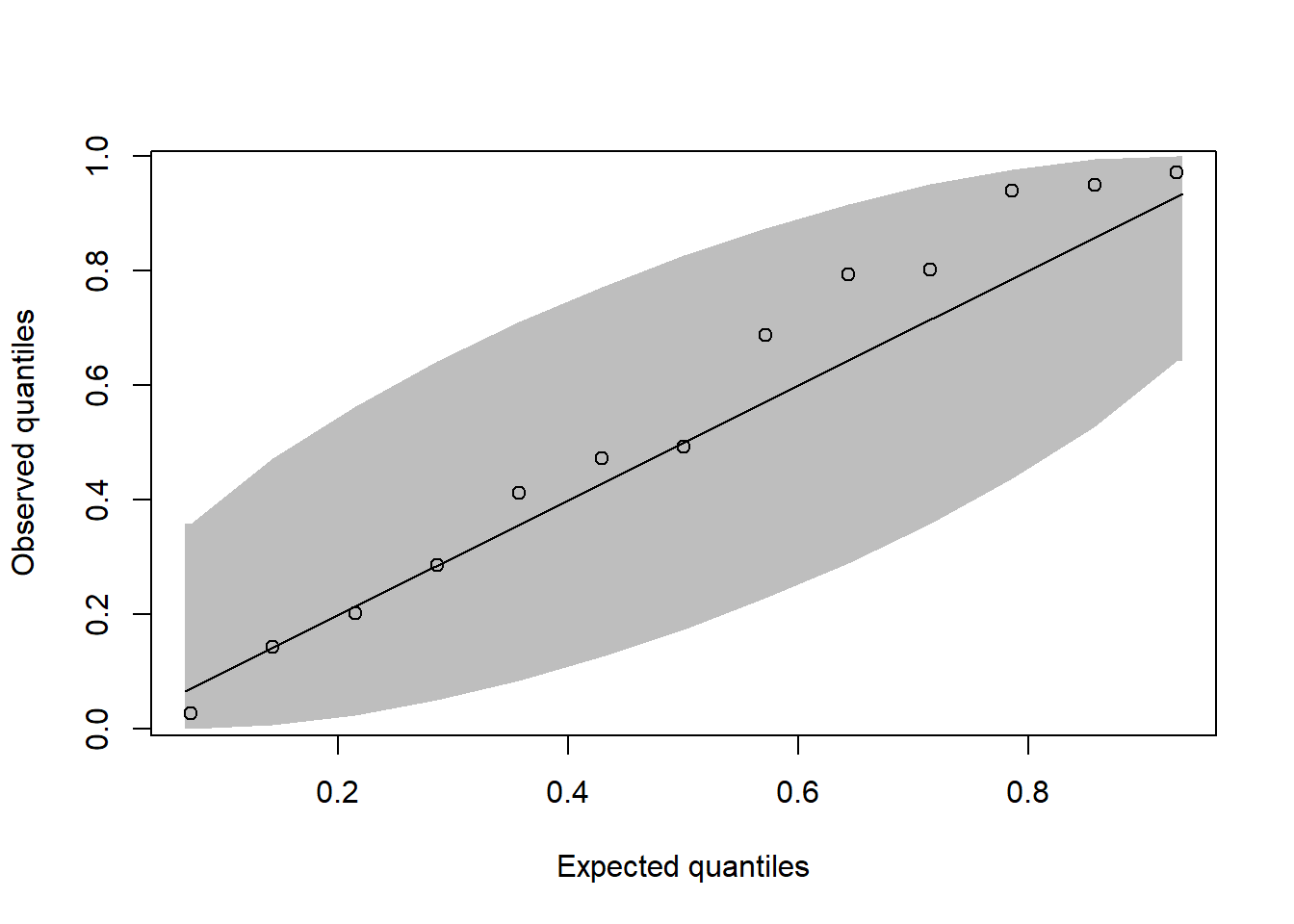
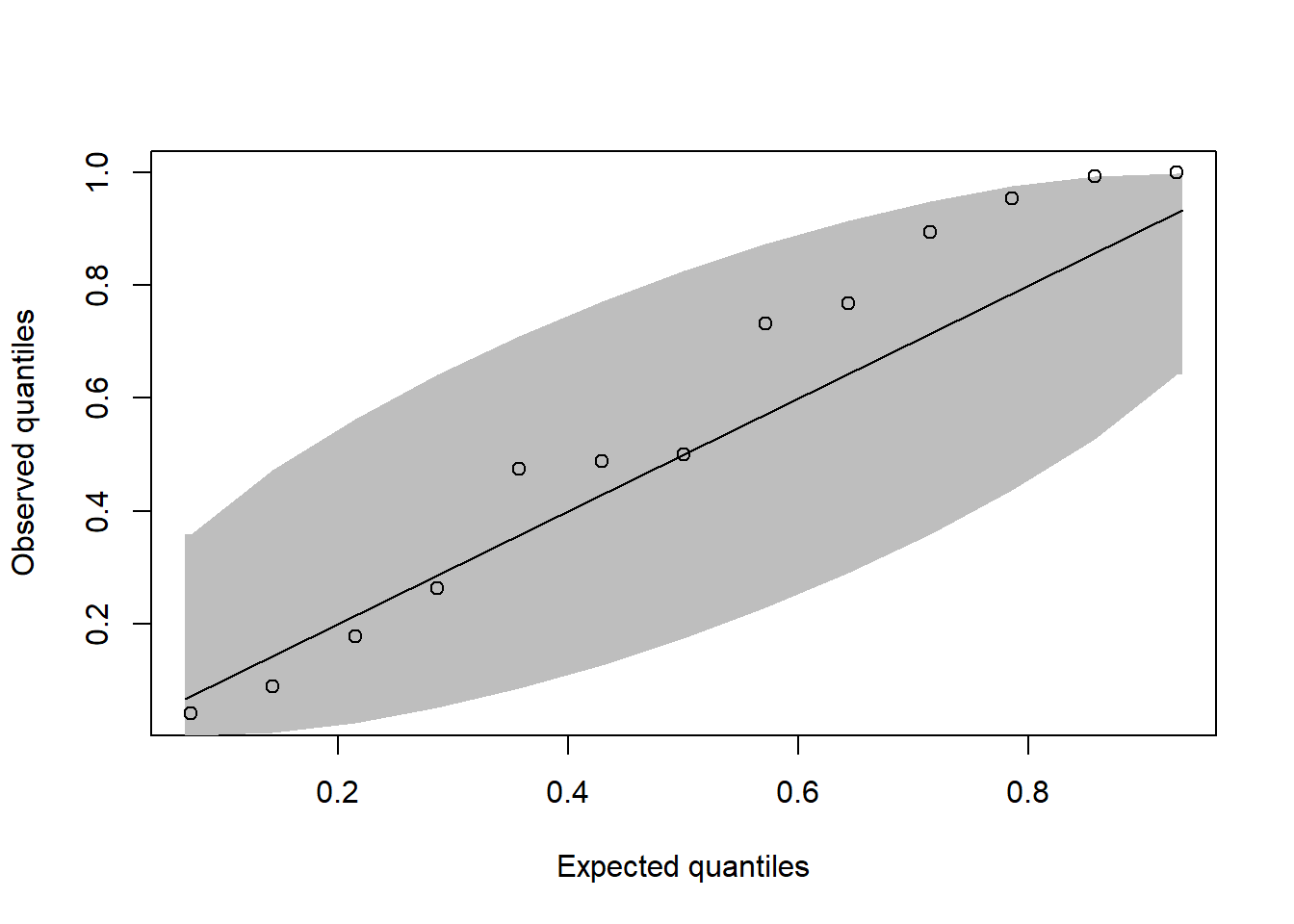
coe <- readRDS("data/coe_2025-07-14.rds")

# Select studies / conditions
data <- subset(coe, coe$Experimental == TRUE)

knitr::kable(data)
Study Experimental N Trials Labstudy MaxBF MaxBF p Energy Energy p FFT Amplitude sum FFT p Direction Year
1 Loving Kind TRUE 171 100 TRUE 4.16 (n=32) 0.113 17.3323658 0.155 3.2230266 0.120 greater 2016
2 Prayer TRUE 431 100 FALSE 1.44 (n=17) 0.481 -269.8522810 0.723 1.4152882 0.481 greater 2017
3 Monks T1 Exp TRUE 23 400 TRUE 1.98 (n=22) 0.139 6.4433144 0.109 1.8132058 0.124 greater 2016
5 Monks T2 Exp TRUE 23 400 TRUE 1.74 (n=14) 0.169 4.1145076 0.136 1.5355084 0.176 greater 2016
8 Meditation T2 TRUE 48 100 FALSE 1.74 (n=4) 0.248 -13.4776043 0.571 1.3364722 0.324 greater 2016
9 Sound preference TRUE 70 40 TRUE 1.27 (n=53) 0.502 -1.2866724 0.310 1.3444904 0.413 greater 2017
10 All-will-be-good TRUE 38 100 TRUE 1.77 (n=5) 0.233 -9.0209420 0.539 1.4316730 0.267 greater 2016
11 One-armed Bandit TRUE 40 200 TRUE 4.15 (n=24) 0.053 44.7542814 0.023 3.8722029 0.036 greater 2017
12 Coin Toss TRUE 40 200 TRUE 1.15 (n=17) 0.494 -2.6510812 0.309 1.1980540 0.415 greater 2017
13 Incongruence Exp TRUE 236 10 FALSE 10.72 (n=153) 0.034 564.2794225 0.014 9.8855220 0.023 greater 2017
15 Smokers 1 Exp TRUE 122 400 TRUE 66.06 (n=122) 0.007 497.5324261 0.006 44.3077124 0.006 different 2015
17 Smokers 2 Exp TRUE 175 400 TRUE 10.19 (n=7) 0.055 -59.1807244 0.117 6.9914349 0.052 less 2016
19 Smokers 3 TRUE 203 400 TRUE 1.89 (n=3) 0.248 -130.0131545 0.259 1.3069516 0.298 less 2017
20 Psyscanner Style 1 Exp TRUE 1400 30 FALSE 12.92 (n=825) 0.041 4219.9909834 0.017 17.4089785 0.024 greater 2018
22 Psyscanner Style 2 Exp TRUE 1308 30 FALSE 3.2 (n=355) 0.234 -100.5866340 0.185 3.6257502 0.202 greater 2018
24 Psyscanner Style 3 Exp TRUE 1462 30 FALSE 2.39 (n=187) 0.341 -335.8538173 0.241 2.9555095 0.261 greater 2018
26 Relaxation TRUE 12571 100 FALSE 7.44 (n=380) 0.110 -6613.7973890 0.110 7.5178618 0.093 greater 2016
27 Priming 1 Exp TRUE 4092 20 FALSE 28.78 (n=1680) 0.023 13019.9850265 0.019 32.3122569 0.020 greater 2018
29 Priming 2 Exp TRUE 2063 20 FALSE 1.15 (n=21) 0.767 -1698.4653454 0.903 1.1666602 0.868 greater 2018
31 Priming 3 Exp TRUE 6099 20 FALSE 1.01 (n=28) 0.868 -5344.8881540 0.826 1.2224719 0.844 greater 2019
33 Priming 4 Exp TRUE 4060 20 FALSE 1.65 (n=11) 0.539 -3516.5425960 0.884 1.5013128 0.656 greater 2020
35 Erotic Images 1 TRUE 241 200 FALSE 1.39 (n=111) 0.492 -54.6198230 0.288 1.4261007 0.446 greater 2017
36 Erotic Images 2 TRUE 678 50 FALSE 5.24 (n=363) 0.111 482.4092013 0.053 5.2927945 0.101 greater 2017
37 Smokers Priming Exp TRUE 38 20 TRUE 1.76 (n=4) 0.203 -0.2905169 0.345 1.5031201 0.248 greater 2021
44 Robots TRUE 34 10 FALSE 2.28 (n=13) 0.150 10.8768366 0.113 2.1187153 0.125 greater 2023
45 Schrödingers Cat Exp TRUE 285 10 FALSE 1 (n=1) 1.000 -212.2066205 0.986 0.8261145 1.000 greater 2023
46 Schrödingers Cat Con TRUE 285 10 FALSE 1.87 (n=104) 0.327 -15.6696056 0.172 1.9681821 0.279 greater 2023
47 Desire TRUE 201 10 FALSE 1.45 (n=14) 0.440 -41.5934015 0.282 1.5823083 0.352 greater 2023
48 Stories TRUE 766 1 FALSE 2.18 (n=207) 0.305 -39.9578792 0.129 2.7597607 0.195 greater 2023
49 Willpower TRUE 703 20 FALSE 15.68 (n=58) 0.024 193.4717104 0.126 10.2119849 0.035 greater 2023
50 Baseline 1 Lucky TRUE 801 20 FALSE 13.21 (n=627) 0.032 1588.9475978 0.020 14.5909943 0.023 less 2024
51 Baseline 1 Unlucky TRUE 725 20 FALSE 1 (n=1) 1.000 -518.3810925 0.810 0.9199984 0.960 greater 2024
52 Baseline 2 TRUE 2094 20 FALSE 4.04 (n=6) 0.161 -1539.0855934 0.615 2.3741518 0.280 less 2024 
istwo <- ifelse(data$Direction == "different", TRUE, FALSE) # two-tailed test
df <- data$N-1 # degrees of freedom

library(metap)

Max BF

pvals <- two2one(data$`MaxBF p`, istwo)

res <- invchisq(pvals, k=df)
print(res)
chisq =  41336.33  with df =  41493  p =  0.706167 
plot(res)

BF Energy

pvals <- two2one(data$`Energy p`, istwo)

res <- invchisq(pvals, k=df)
print(res)
chisq =  42142.89  with df =  41493  p =  0.01233156 
plot(res)

FFT Amplitude Sum

pvals <- two2one(data$`FFT p`, istwo)

res <- invchisq(pvals, k=df)
print(res)
chisq =  42011.57  with df =  41493  p =  0.03632617 
plot(res)

Robustness to Sample Sizes

In comparison to the inverse chi-square method, which weights each p-value by its degree of freedom and therefor its sample size, Fisher’s method combines p-values by taking the sum of their logarithms and then comparing them to a chi-square distribution. This method is less sensitive to sample sizes and can be used as a robustness check countering arguments of selectively continuing data collection of studies with a noticeable BF.

#Max BF
pvals <- two2one(data$`MaxBF p`, istwo)
sumlog(pvals)
chisq =  116.8555  with df =  66  p =  0.0001159669 
#Energy BF
pvals <- two2one(data$`Energy p`, istwo)
sumlog(pvals)
chisq =  120.4762  with df =  66  p =  4.881634e-05 
#FFT Amplitude Sum
pvals <- two2one(data$`FFT p`, istwo)
sumlog(pvals)
chisq =  121.2422  with df =  66  p =  4.051184e-05

In this analysis all Micro-Pk studies of the LMU Micro-Pk Lab are included that hypothesize the absence of an effect. In studies comparing experimental to control conditions, only the control conditions are included.

# Select studies / conditions
data <- subset(coe, coe$Experimental == FALSE)
knitr::kable(data)
Study Experimental N Trials Labstudy MaxBF MaxBF p Energy Energy p FFT Amplitude sum FFT p Direction Year
4 Monks T1 Con FALSE 29 400 TRUE 1 (n=1) 1.000 -9.659564 0.786 0.9418921 0.899 greater 2016
6 Monks T2 Con FALSE 29 400 TRUE 1.18 (n=7) 0.440 -5.080576 0.469 1.0954834 0.495 greater 2016
7 Meditation T1 FALSE 40 100 FALSE 1 (n=1) 1.000 -17.858023 0.938 0.8598144 1.000 greater 2016
14 Incongruence Con FALSE 271 10 FALSE 2.1 (n=125) 0.289 -7.056369 0.171 2.0230283 0.265 greater 2017
16 Smokers 1 Con FALSE 132 400 TRUE 1 (n=1) 1.000 -99.068118 0.987 0.8035244 0.999 different 2015
18 Smokers 2 Con FALSE 220 400 TRUE 6.97 (n=10) 0.080 -80.293313 0.111 4.4652477 0.086 less 2016
21 Psyscanner Style 1 Con FALSE 1003 30 FALSE 1.12 (n=2) 0.735 -483.528052 0.449 1.2492501 0.755 greater 2018
23 Psyscanner Style 2 Con FALSE 1095 30 FALSE 7.84 (n=936) 0.087 1605.391713 0.042 9.0438404 0.060 greater 2018
25 Psyscanner Style 3 Con FALSE 941 30 FALSE 3.72 (n=17) 0.181 -572.637818 0.637 2.4770702 0.298 greater 2018
28 Priming 1 Con FALSE 4092 20 FALSE 1.38 (n=58) 0.648 -3306.742875 0.687 1.3074276 0.768 greater 2018
30 Priming 2 Con FALSE 2063 20 FALSE 1 (n=1) 1.000 -1611.962028 0.801 0.9568926 0.994 greater 2018
32 Priming 3 Con FALSE 6099 20 FALSE 1 (n=1) 1.000 -5561.551895 0.949 1.0836289 0.955 greater 2019
34 Priming 4 Con FALSE 4060 20 FALSE 1.56 (n=5) 0.562 -3668.203466 0.970 1.3702124 0.732 greater 2020
38 Smokers Priming Con FALSE 38 20 TRUE 1.88 (n=6) 0.164 1.791793 0.287 1.5536720 0.227 greater 2021
39 Sobjectivity 1 FALSE 898 20 FALSE 1.41 (n=2) 0.580 -663.231171 0.893 1.1422082 0.853 greater 2021
40 Sobjectivity 2 FALSE 986 20 FALSE 1 (n=1) 1.000 -775.260879 0.954 0.9212182 0.994 greater 2021
41 Sobjectivity 3 FALSE 1503 20 FALSE 56.51 (n=56) 0.009 975.793930 0.071 47.2555391 0.011 greater 2023
42 Epsi Correlation Condition A FALSE 2052 20 FALSE 1.6 (n=78) 0.529 -1574.744262 0.765 1.4901842 0.631 greater 2021
43 Epsi Correlation Condition B FALSE 2052 20 FALSE 2.47 (n=8) 0.322 -1578.129000 0.769 2.1287147 0.399 greater 2021 
library(metap)
istwo <- ifelse(data$Direction == "different", TRUE, FALSE) # two-tailed test
df <- data$N-1 # degrees of freedom

Max BF

pvals <- two2one(data$`MaxBF p`, istwo)
res <- invchisq(pvals, k=df)
print(res)
chisq =  18595.24  with df =  27584  p =  1 
plot(res)

BF Energy

pvals <- two2one(data$`Energy p`, istwo)
res <- invchisq(pvals, k=df)
print(res)
chisq =  27103.61  with df =  27584  p =  0.9800317 
plot(res)

FFT Amplitude Sum

pvals <- two2one(data$`FFT p`, istwo)
res <- invchisq(pvals, k=df)
print(res)
chisq =  27152.37  with df =  27584  p =  0.9674448 
plot(res)

Robustness to Sample Sizes

#Max BF
pvals <- two2one(data$`MaxBF p`, istwo)
sumlog(pvals)
chisq =  39.16682  with df =  38  p =  0.4172743 
#Energy BF
pvals <- two2one(data$`Energy p`, istwo)
sumlog(pvals)
chisq =  30.83717  with df =  38  p =  0.7887142 
#FFT Amplitude Sum
pvals <- two2one(data$`FFT p`, istwo)
sumlog(pvals)
chisq =  35.51057  with df =  38  p =  0.5851368